温斯顿吴的个人博客 woojean.com

编程问题总结-Algorithm

2017-04-05
编程

选择排序（C）

首先找到最小元素置于起始位置，再从剩余元素中继续寻找最小者放到已排序序列末尾，依次类推（不稳定排序）

void SelectionSort(int arr[],int len){
  
  int i,j,min,tmp;

  for(i = 0; i < len; i++){
    min = i;
    for(j = i; j < len; j++){
      if(arr[j] < arr[min]){
        min = j;
      }
    }
    tmp = arr[i];
    arr[i] = arr[min];
    arr[min] = tmp;
  }
}

插入排序（C）

对于未排序数据在已排序序列中从后向前扫描，找到相应位置并插入（稳定排序）

void InsertionSort(int arr[],int len){
  
  int i,j,tmp;

  for(i = 1; i < len; i++){
    tmp = arr[i];
    for(j = i; j>0 && arr[j-1]>tmp; j--){
      arr[j] = arr[j-1];
      arr[j-1] = tmp;
    }
  }
}

冒泡排序（C）

（稳定排序）

void BubbleSort(int arr[],int len){
  
  int i,j,tmp;

  for(i = 0; i < len; i++){
    for(j = i+1; j < len; j++){
      if(arr[j] < arr[i]){
        tmp = arr[j];
        arr[j] = arr[i];
        arr[i] =tmp;
      }
    }
  }
}

希尔排序（C）

插入排序的变种。 先取一个正整数d1 < N，把所有相隔d1的元素放一组，共d1组，组内进行直接插入排序，再取d2 < d1，重复上述步骤，直至d=1.只要最终步长为1，任何步长序列都可以，当步长为1时，算法即为插入排序。（不稳定排序）

void ShellSort(int arr[],int len){
  
  int i,j,incr,tmp;
  
  // 14,7,3,1
  for(incr = len/2; incr > 0; incr /= 2){
    for(i = incr; i < len; i++){
      tmp = arr[i];
      for(j = i; j >= incr; j -= incr){
        if(tmp < arr[j-incr]){
          arr[j] = arr[j-incr];
        }
        else{
          break;
        }
      }
      arr[j] = tmp;
    }
  }
}

快速排序（C）

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。 （不稳定排序）

void QuickSort(int a[],int low,int high){
  
  int i = low;
  int j = high;  
  int temp = a[i]; 
  
  if( low < high){          
    while(i < j)  // 若条件为i<=j，则将所有判定都加等号则会发生死循环
    {
      while((a[j] >= temp) && (i < j)){ 
        j--; 
      }
      a[i] = a[j];

      while((a[i] <= temp) && (i < j)){
        i++; 
      }  
      a[j]= a[i];  
    }
    a[i] = temp;
    QuickSort(a,low,i-1);
    QuickSort(a,j+1,high);
  }
}

第二种

void qsort(int v[], int left, int right){
  int i,last;
  void swap(int v[],int i,int j);

  if(left >= right){
    return ;
  }

  swap(v,left,(left + right)/2);
  last = left;
  for(i = left +1; i<= right; i++){
    if(v[i] < v[left]){
      swap(v, ++last,i);
    }
  }
  swap(v, left, last);
  qsort(v,left,last-1);
  qsort(v,last+1,right);
}

void swap(int v[], int i, int j){
  int temp;
  temp = v[i];
  v[i] = v[j];
  v[j] = temp;
}

归并排序（C）

（稳定排序）

void  Merge( int arr[], int tmpArray[], int lBegin, int rBegin, int rEnd )
{
  int i, lEnd, len, tmpPos;
  lEnd = rBegin - 1;
  tmpPos = lBegin;
  len = rEnd - lBegin + 1;
  
  /* main loop */
  while( lBegin <= lEnd && rBegin <= rEnd ){
    if( arr[ lBegin ] <= arr[ rBegin ] ){
      tmpArray[ tmpPos++ ] = arr[ lBegin++ ];
    }
    else{
      tmpArray[ tmpPos++ ] = arr[ rBegin++ ];
    }
  }
  while( lBegin <= lEnd ){
    tmpArray[ tmpPos++ ] = arr[ lBegin++ ];
  }

  while( rBegin <= rEnd ){
    tmpArray[ tmpPos++ ] = arr[ rBegin++ ];
  }

  for( i = 0; i < len; i++, rEnd-- ){
    arr[ rEnd ] = tmpArray[ rEnd ];
  }
}


void MSort( int arr[ ], int tmpArray[ ], int left, int right )
{
  int mid;
  if( left < right )
  {
    mid = ( left + right ) / 2;
    MSort( arr, tmpArray, left, mid );
    MSort( arr, tmpArray, mid + 1, right );
    Merge( arr, tmpArray, left, mid + 1, right );
  }
}
       
       
void  MergeSort( int arr[ ], int len )
{
  int *tmpArray;
  tmpArray = malloc( len * sizeof( int ) );
  if( tmpArray != NULL )
  {
    MSort( arr, tmpArray, 0, len - 1 );
    free( tmpArray );
  }
  else
    printf( "No space for tmp array!!!" );
}

堆排序（C）

（不稳定排序）

#define LeftChild(i)  (2*(i) + 1)

//对数组A中以下标为i的元素作为根，大小为len的元素序列构成的堆进行堆调整，使该根节点放到合适的位置
void Sink(int arr[],int i,int len){
  int child,tmp;

  for(tmp = arr[i]; LeftChild(i)<len; i=child){
    child = LeftChild(i);

    if( child != len-1 && arr[child+1] > arr[child]){
      child++;
    }

    if( tmp < arr[child] ){
      arr[i] = arr[child];
    }
    else{
      break;
    }
  }
  arr[i] = tmp;
}

void HeapSort(int arr[],int len){
  int i,tmp;
  for( i = len/2; i >= 0; i-- ){  // BuildHeap从下往上建堆
    Sink( arr, i, len );
  }
  
  // 取大根堆的根（即最大元素）放到数组末尾，同时缩减数组长度
  for( i = len - 1; i > 0; i-- ){ 
    /* DeleteMax */
    tmp = arr[0];
    arr[0] = arr[i];
    arr[i] = tmp;
    Sink( arr, 0, i );
  }

}

计数排序（C）

（稳定排序）

void CountingSort(int arr[],int len){
  
  int i, min, max;
  min = max = arr[0];

  // 找出范围
  for(i = 1; i < len; i++) {
    if (arr[i] < min)
      min = arr[i];
    else if (arr[i] > max)
      max = arr[i];
  }
  int range = max - min + 1;
  
  int *count = (int*)malloc(range * sizeof(int));
  for(i = 0; i < range; i++){
    count[i] = 0;
  }
  for(i = 0; i < len; i++){
    count[ arr[i] - min ]++;
  }
  
  int j, z = 0;
  for(i = min; i <= max; i++){
    for(j = 0; j < count[ i - min ]; j++){
      arr[z++] = i;
    }
  }
  free(count);
}

二分查找法（C）

int HalfSearch(int arr[], int low, int high, int num){
  int mid;
  mid = (low+high) / 2;
  if( (low>=high) && (arr[mid]!=num) ){
    return -1;
  }
  else{
    if( arr[mid]==num ){
      return mid;
    }
    else if( arr[mid]>num ){
      high = mid-1;
    }
    else{ 
      low = mid+1;
    }
    return HalfSearch(arr,low,high,num);
  }
}

前序遍历二叉树

遍历二叉树的算法中基本操作是访问结点，因此，无论是哪种次序的遍历，对有n个结点的二叉树，其时间复杂度均为O(n) 。 递归算法:

void PreorderTraverse(BTNode  *T){  
  if( T!=NULL ){  
    visit(T->data) ;       // 访问根结点
    PreorderTraverse(T->Lchild) ;
    PreorderTraverse(T->Rchild) ;     
  }
}

非递归算法: 设T是指向二叉树根结点的指针变量，非递归算法是： 若二叉树为空，则返回；否则，令p=T； ⑴ 访问p所指向的结点； ⑵ q=p->Rchild ，若q不为空，则q进栈； ⑶ p=p->Lchild ，若p不为空，转(1)，否则转(4)； ⑷ 退栈到p ，转(1)，直到栈空为止。

#define  MAX_NODE  50
void PreorderTraverse( BTNode  *T){  
  BTNode *Stack[MAX_NODE] , *p=T,  *q ;
  int  top=0 ;
  if  (T==NULL){  
    printf(“ Binary Tree is Empty!\n”) ;
  }
  else {  
    do{  
      visit( p-> data ) ;   
      q=p->Rchild ; 
      if ( q!=NULL ){  
        Stack[++top]=q ;
      }          
      p=p->Lchild ; 
      if (p==NULL){ 
        p=Stack[top--] ;  
      }  
    }
    while (p!=NULL) ;
  }
}

中序遍历二叉树

递归算法

void  InorderTraverse(BTNode  *T){  
  if (T!=NULL){  
    InorderTraverse(T->Lchild) ;
    visit(T->data) ;       // 访问根结点
    InorderTraverse(T->Rchild) ;
  }
}

中序遍历二叉树（非递归算法） 设T是指向二叉树根结点的指针变量，非递归算法是： 若二叉树为空，则返回；否则，令p=T ⑴ 若p不为空，p进栈， p=p->Lchild ；否则(即p为空)，退栈到p，访问p所指向的结点； ⑵ p=p->Rchild ，转(1)； 直到栈空为止。

#define MAX_NODE  50
void  InorderTraverse( BTNode  *T){  
  BTNode  *Stack[MAX_NODE] ,*p=T ;
  int top=0 , bool=1 ;
  if (T==NULL){  
    printf(“ Binary Tree is Empty!\n”) ;
  }  
  else{ 
    do{ 
      while (p!=NULL){  
        stack[++top]=p ;    
        p=p->Lchild ;   
      }
      if (top==0){  
        bool=0 ;
      }
      else{  
        p=stack[top--] ;  
        visit( p->data ) ;  
        p=p->Rchild ; 
      }
    } while (bool!=0) ;
  }
 }

后序遍历二叉树

递归算法

void  PostorderTraverse(BTNode  *T){  
  if (T!=NULL) {  
    PostorderTraverse(T->Lchild) ;
    PostorderTraverse(T->Rchild) ; 
    visit(T->data) ;   // 访问根结点 
  }
}

设T是指向根结点的指针变量，后序遍历二叉树的非递归算法是： 若二叉树为空，则返回；否则，令p=T； ⑴ 第一次经过根结点p，不访问： p进栈S1 ， tag 赋值0，进栈S2，p=p->Lchild 。 ⑵ 若p不为空，转(1)，否则，取状态标志值tag； ⑶ 若tag=0：对栈S1，不访问，不出栈；修改S2栈顶元素值(tag赋值1) ，取S1栈顶元素的右子树，即p=S1[top]->Rchild ，转(1)； ⑷ 若tag=1：S1退栈，访问该结点； 直到栈空为止。

层序遍历二叉树（C）

#define MAX_NODE  50
void LevelorderTraverse( BTNode  *T){  
  BTNode  *Queue[MAX_NODE] ,*p=T ;
  int  front=0 , rear=0 ;
  if (p!=NULL){  
    Queue[++rear]=p;    // 根结点入队
    
    // 当队列不为空时
    while (front < rear){  
      p = Queue[++front];
      visit( p->data );
      if (p->Lchild!=NULL){
        Queue[++rear]=p;  // 左结点入队
      }                  
      if (p->Rchild!=NULL){
        Queue[++rear]=p;  // 右结点入队
      }          
    }
  }
}

判断二叉树是否相等（C）

typedef struct _TreeNode{
  char c;
  TreeNode *leftchild;
  TreeNode *rightchild;
}TreeNode;

// A、B两棵树相等当且仅当RootA->c==RootB-->c,而且A和B的左右子树相等或者左右互换相等。
int CompTree(TreeNode* tree1,TreeNode* tree2){
  if( tree1==NULL && tree2 == NULL ){
    Return 0;
  }
  if( tree1 == NULL || tree2 == NULL ){
    return 1;
  }
  if( tree1->c != tree2->c){
    return 1;
  }
  
  if( CompTree(tree1->leftchild, tree2->leftchild) == 0  && CompTree(tree1->rightchild, tree2->rightchild) == 0 ){
    return 0;
  }

  if( CompTree(tree1->leftchild, tree2->rightchild) == 0 && CompTree(tree1->rightchild, tree2->leftchild) == 0 ){
    return 0;
  }
}

由于需要比较的状态是两棵树的任意状态，而二叉树上的每一个节点的左右子节点都可以交换，因此一共需要对比2^n种状态。算法复杂度是O（2^n）

求二叉树的叶子节点数（C）

#define  MAX_NODE  50
int search_leaves( BTNode  *T){  
  BTNode  *Stack[MAX_NODE] ,*p=T;
  int top=0, num=0;
  if(T!=NULL){  
    stack[++top]=p ; 
    while( top > 0 ){  
      p = stack[top--] ;
      if( p->Lchild==NULL && p->Rchild==NULL ){
        num++ ;
      }   
      if( p->Rchild != NULL ){
        stack[++top]=p->Rchild; 
      }  
      if(p->Lchild != NULL ){
        stack[++top]=p->Lchild; 
      } 
    }
  }
  return(num) ;
}

求二叉树的深度（C）

#define MAX_NODE 50
int search_depth( BTNode  *T){  
  BTNode  *Stack[MAX_NODE] ,*p=T;
  int  front=0 , rear=0, depth=0, level ;
  
  // level总是指向访问层的最后一个结点在队列的位置
  if (T!=NULL){  
    Queue[++rear]=p;    // 根结点入队
    level=rear ;    // 根是第1层的最后一个节点
    while (front < rear){  
      p=Queue[++front]; 
      if (p->Lchild != NULL){
        Queue[++rear]=p;    // 左结点入队
      }                  
      if (p->Rchild!=NULL){
        Queue[++rear]=p;    // 右结点入队
      }              
      if (front == level){  
        // 正访问的是当前层的最后一个结点
        depth++ ;  
        level=rear ;  
      }
    }
  }
}

求最大的子序 列和的联机算法（C）

int  MaxSubSequenceSum(const int arr[],int len){
  int  tmpSum, maxSum, j;
  tmpSum = maxSum = 0;
  
  for( j=0; j<len; j++ ){
    tmpSum += arr[j];
    if(tmpSum > maxSum){
      maxSum = tmpSum;
    }
    else if(tmpSum < 0){
      tmpSum = 0;
    }
  }
  return maxSum;
}

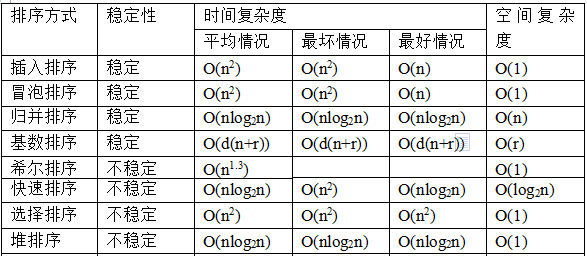
分析排序算法时间空间复杂度和各自的稳定性

image

写内存拷贝

void * memcpy (void * dst, const void * src, size_t count){
  
  void * ret = dst;
  
  while (count--) {
    *(char *)dst = *(char *)src;
    dst = (char *)dst + 1;
    src = (char *)src + 1;
  }
  return(ret);
}

图的广度优先遍历（C）

(1)邻接表表示图的广度优先搜索算法

// 以vk为源点对用邻接表表示的图G进行广度优先搜索
void BFS(ALGraph*G，int k){
  int i;
  CirQueue Q;    //须将队列定义中DataType改为int
  EdgeNode *p;
  InitQueue(&Q); //队列初始化
  printf("visit vertex：％e",G->adjlist[k].vertex); //访问源点vk
  visited[k]=TRUE; 
  EnQueue(&Q，k); //vk已访问，将其人队。（实际上是将其序号人队）
  while(!QueueEmpty(&Q)){ //队非空则执行
    i=DeQueue(&Q); //相当于vi出队
    p=G->adjlist[i].firstedge; //取vi的边表头指针
    while(p){ //依次搜索vi的邻接点vj(令p->adjvex=j)
      if(!visited[p->adivex]){ //若vj未访问过
        printf("visitvertex：％c",C->adjlistlp->adjvex].vertex); //访问vj
        visited[p->adjvex]=TRUE; 
        EnQueue(&Q，p->adjvex);//访问过的vj人队
      }//endif
      p=p->next; //找vi的下一邻接点
    }//endwhile
  }//endwhile
}//end of BFS

（2）邻接矩阵表示的图的广度优先搜索算法

// 以vk为源点对用邻接矩阵表示的图G进行广度优先搜索
void BFSM(MGraph *G，int k){
  int i,j;
  CirQueue Q;
  InitQueue(&Q);
  printf("visit vertex:％c",G->vexs[k]); //访问源点vk
  visited[k]=TRUE;
  EnQueue(&Q,k);
  while(!QueueEmpty(&Q)){
    i=DeQueue(&Q); //vi出队
    //依次搜索vi的邻接点vj
    for(j=0;j<G->n;j++){
      if(G->edges[i][j]==1&&!visited[j]){ //vi未访问
        printf("visit vertex:％c"，G->vexs[j]);//访问vi
        visited[j]=TRUE;
        EnQueue(&Q,j);//访问过的vi人队
      }
    }
  }//endwhile
}//BFSM

对于具有n个顶点和e条边的无向图或有向图，每个顶点均入队一次。广度优先遍历(BFSTraverse)图的时间复杂度和DFSTraverse算法相同。 当图是连通图时，BFSTraverse算法只需调用一次BFS或BFSM即可完成遍历操作，此时BFS和BFSM的时间复杂度分别为O(n+e)和0(n2)。

图的深度优先遍历（C）

（1）深度优先遍历算法

typedef enum{FALSE，TRUE} Boolean;  // FALSE为0，TRUE为1
Boolean visited[MaxVertexNum]; // 访问标志向量是全局量
    
// 深度优先遍历以邻接表表示的图G，而以邻接矩阵表示G时，算法完全与此相同
void DFSTraverse(ALGraph *G){ 
  int i;
  for(i=0;i<G->n;i++){
    visited[i]=FALSE; //标志向量初始化
  }
    
  for(i=0; i<G->n; i++){
    if(!visited[i]){ //vi未访问过
      DFS(G，i)； //以vi为源点开始DFS搜索
    }
  }
}

（2）邻接表表示的深度优先搜索算法

void DFS(ALGraph *G，int i){ 
  // 以vi为出发点对邻接表表示的图G进行深度优先搜索
  EdgeNode *p;
  printf("visit vertex：％c"，G->adjlist[i].vertex);  //访问顶点vi
  visited[i]=TRUE; //标记vi已访问
  p=G->adjlist[i].firstedge; // 取vi边表的头指针
  while(p){ //依次搜索vi的邻接点vj，这里j=p->adjvex
    if (!visited[p->adjvex]){// 若vi尚未被访问
      DFS(G，p->adjvex);//则以Vj为出发点向纵深搜索
    }
    p=p->next; // 找vi的下一邻接点
  }
}

（3）邻接矩阵表示的深度优先搜索算法

void DFSM(MGraph *G，int i){ 
  // 以vi为出发点对邻接矩阵表示的图G进行DFS搜索，设邻接矩阵是0,l矩阵
  int j;
  printf("visit vertex：％c"，G->vexs[i]); //访问顶点vi
  visited[i]=TRUE;
  for(j=0;j<G->n;j++){ //依次搜索vi的邻接点
    if(G->edges[i][j]==1&&!visited[j]){
        DFSM(G，j)//(vi，vj)∈E，且vj未访问过，故vj为新出发点
    }
  }
}

对于具有n个顶点和e条边的无向图或有向图，遍历算法DFSTraverse对图中每顶点至多调用一次DFS或DFSM。从DFSTraverse中调用DFS(或DFSM)及DFS(或DFSM)内部递归调用自己的总次数为n。 当访问某顶点vi时，DFS(或DFSM)的时间主要耗费在从该顶点出发搜索它的所有邻接点上。用邻接矩阵表示图时，其搜索时间为O(n)；用邻接表表示图时，需搜索第i个边表上的所有结点。因此，对所有n个顶点访问，在邻接矩阵上共需检查n2个矩阵元素，在邻接表上需将边表中所有O(e)个结点检查一遍。 所以，DFSTraverse的时间复杂度为O(n2) （调用DFSM）或0(n+e)（调用DFS）。

图的邻接矩阵存储结构形式说明（C）

#define MaxVertexNum l00
typedef struct{
  char vexs[MaxVertexNum];   // 顶点表
  int edges[MaxVertexNum][MaxVertexNum]; // 邻接矩阵，可看作边表
  int n,e; // 图中当前的顶点数和边数
}MGragh;

图的邻接表的形式说明及其建表算法（C）

对图的每个顶点建立一个单链表（n个顶点建立n个单链表），第i个单链表中的结点包含顶点Vi的所有邻接顶点。又称链接表。 （1）邻接表的形式说明

// 边表结点
typedef struct node{ 
  int adjvex; // 邻接点域
  struct node *next; // 链域
  // 若要表示边上的权，则应增加一个数据域
}EdgeNode;

// 顶点表结点
typedef struct vnode{  
  int vertex; // 顶点域
  EdgeNode *firstedge;  // 边表头指针
}VertexNode;

typedef VertexNode AdjList[MaxVertexNum]; //AdjList是邻接表类型

（2）建立无向图的邻接表算法

// 建立无向图的邻接表表示
void CreateALGraPh(ALGrahp *G){
  int i,j,k;
  EdgeNode *s；
  scanf("％d％d"，&G->n，&G->e); // 读入顶点数和边数
  for(i=0;i<G->n;i++){
    //建立顶点表
    G->adjlist[i].vertex=getchar(); //读入顶点信息
    G->adjlist[i].firstedge=NULL;//边表置为空表
  }
      
  for(k=0; k<G->e; k++){
    //建立边表
    scanf("％d％d",&i,&j);否则读入边(vi，vj)的顶点对序号
    s=(EdgeNode *)malloc(sizeof(EdgeNode));  //生成边表结点
    s->adjvex=j; //邻接点序号为j
    s->next=G->adjlist[i].firstedge;
    G->adjlist[i].firstedge=s; //将新结点*s插入顶点vi的边表头部
    s=(EdgeNode *)malloc(sizeof(EdgeNode));
    s->adjvex=i; //邻接点序号为i
    s->next=G->adjlist[j].firstedge;
    G->adjlistk[j].firstedge=s; //将新结点*s插入顶点vj的边表头部
  }//end for 
}CreateALGraph

排序相关问题

1.基于比较的排序，其复杂度最佳是多少？ 2.快排排序、归并排序，其复杂度是多少？ 3.既然快排O(n^2) > O(nlogn), 为什么实际应用中，快排的表现经常优于归并排序？ 4.存在O(n)级别的排序算法么？ 答案： 1.O(nlogn) 2.快排O(n^2)，归并排序O(nlogn) 3.inplace、cache性能好 4.存在，非比较排序。如counting sort, radix sort。 （最基础的问题，必须正确。）

说明链表和数组作为数据的不同组织形式，各自的优缺点

数组，在内存上给出了连续的空间。链表，内存地址上可以是不连续的，每个链表的节点包括原来的内存和下一个节点的信息(单向的一个，双向链表的话，会有两个)。

数组优于链表的 1.内存空间占用的少，因为链表节点会附加上一块或两块下一个节点的信息。但是数组在建立时就固定了。所以也有可能会因为建立的数组过大或不足引起内存上的问题。 2.数组内的数据可随机访问，但链表不具备随机访问性。这个很容易理解，数组在内存里是连续的空间，比如如果一个数组地址从100到200，且每个元素占用两个字节，那么100-200之间的任何一个偶数都是数组元素的地址，可以直接访问。链表在内存地址可能是分散的。所以必须通过上一节点中的信息找能找到下一个节点。 3.查找速度。

链表优于数组的 1.插入与删除的操作。如果数组的中间插入一个元素，那么这个元素后的所有元素的内存地址都要往后移动。删除的话同理。只有对数据的最后一个元素进行插入删除操作时，才比较快。链表只需要更改有必要更改的节点内的节点信息就够了。并不需要更改节点的内存地址。

2.内存地址的利用率方面。不管你内存里还有多少空间，如果没办法一次性给出数组所需的要空间，那就会提示内存不足，磁盘空间整理的原因之一在这里。而链表可以是分散的空间地址。

3.链表的扩展性比数组好。因为一个数组建立后所占用的空间大小就是固定的，如果满了就没法扩展，只能新建一个更大空间的数组;而链表不是固定的，可以很方便的扩展。

链表反转（C）

struct Item{
    char c;
    Item *next;
};

Item *Reverse( Item *x ){
    Item *prev = NULL,*curr = x;
    while ( curr ){
        Item *next = curr->next;
        curr->next = prev;
        prev = curr;
        curr = next;
    }
    return prev;
}

int main(){
    Item *x,
        d = {"d", Null},
        c = {"c", &d},
        b = {"b", &c},
        a = {"a", &b};
    x = Reverse( &a );
}

红黑树定义

上一篇 《运营之光》读书笔记

下一篇 编程问题总结-C

文章目录